β（ベータ）とは、株式市場全体の利回りが変化したときに、特定企業の株式の利回りがどれだけ変化するかを表す係数である。イメージ的には、平均株価が10%上昇したときに、特定の株価は何%上昇するかを表す係数ということである（利回りには配当も含むので、この言い方は正確ではないが）。これからも分かるように、βは市場全体の変化に対する個別株式の“感応度”といえる。また、個別株式の利回りのばらつきを表すので、個別株式の“リスク・ファクター”という言い方もできる。βは企業ごとに異なる。

β＝1のときは、個別株式の利回りは、株式市場全体の変動と同じだけ変動する。このような企業は、市場全体と同じ動きをする平均的な企業というイメージだ。

β＞1のときは、個別株式の利回りは、株式市場全体の変動より大きく変動する。景気がいい時には株価は大きく跳ね上がり、景気が悪くなると株価は大きく下がるような企業だ。このような企業の株式は、高い株価が付く可能性がある一方でリスクが高い株式と言える（ハイリスク・ハイリターン）。

0＜β＜1のときは、個別株式の利回りは、株式市場全体の変動ほど変動しない。景気に左右されない、いわゆる「景気に強い企業」のイメージだ。このような企業の株式は、株価が高騰する可能性は低いが、リスクは低い株式と言える（ローリスク・ローリターン）。

β＜0のときは、個別株式の利回りは、株式市場全体の動きと逆の動きをする。すなわち、平均株価が上がるときに、株価が下がる企業だ。このような企業は、現実的にはほとんどない。

少々理論的に言えば、個別株式 \(i\) の利回りと市場全体の利回りの共分散 \( \sigma_{iM}\) を、市場全体の利回りの分散 \( \sigma_{M}^{2}\) で割ったものがβである。 式で書けば以下のようになる。

\[
\beta = \dfrac{\sigma_{iM}}{\sigma_{M}^{2}}
\]

これは、市場全体の利回りと個別株式の利回りの何年分かの実績値を最小自乗法で近似したときの傾きに相当する（下図）。

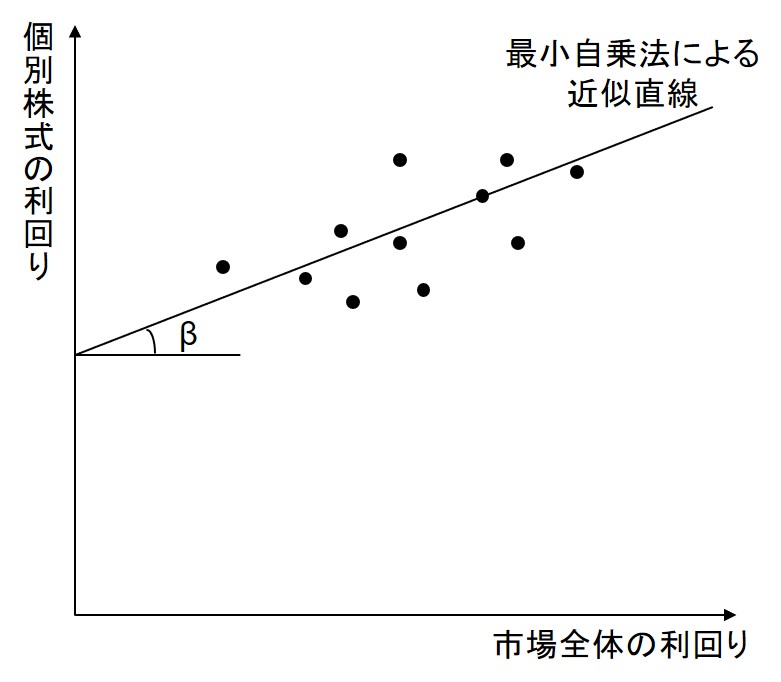
このことから、βとは、市場全体と個別企業の「利回りの比率」ではなく、「利回りの変化の比率」であることが分かるだろう。また、計算期間が同じであれば、1つの企業に対してβは一意に決まる。