将来予想されるキャッシュ・フローの現在価値（→キャッシュの時間価値）の合計額を正味現在価値という。プラスもマイナスを相殺した結果を計算するので「正味」という言葉が付いている。英語ではNet Present Valueといい、略してNPVと言われる。

NPVは投資の評価で用いられる。下図のように、投資額 \(I\) に対して、\(n\) 年間にわたって \(CIF_{1}, CIF_{2}, \cdots, CIF_{n}\) のリターンが見込める投資案件があるとする。

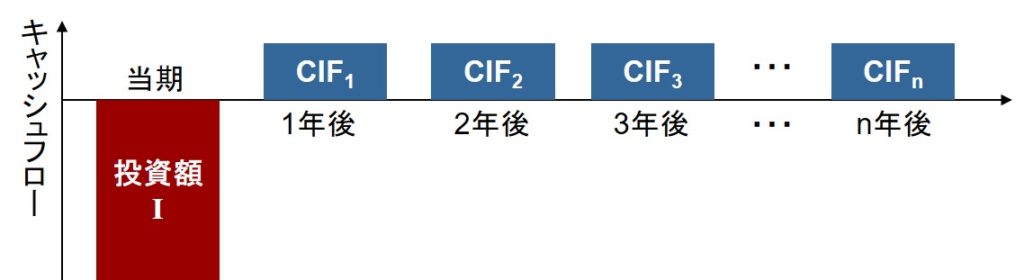
この投資が儲かる場合を最も単純に考えれば、リターンの合計額が投資額を上回る以下の場合である。

\[
\displaystyle \sum_{i}^{n} CIF_{i} \gt I \tag{1}
\]

しかし、キャッシュには時間価値があるので、タイミングが異なるリターンを単純に足すわけにはいかない。時間価値を考慮するには、すべてのキャッシュ・フローをまず投資時点の価値にそろえた上で大小比較すればよい。

割引率（→キャッシュの時間価値）を \(r\) とすれば、以下の場合は投資すべきということになる。

\[
\displaystyle \sum_{i}^{n} \dfrac{CIF_{i}}{(1 + r)^{i}} \gt I \tag{2}
\]

式(2)のように大小比較をしてもいいが、その代わりに差額がプラスであれば投資すると考えても同じである。その差額が正味現在価値（NPV）である。

式で表せは以下のようになる。

\[
\mathrm{NPV} = \displaystyle \sum_{i}^{n} \dfrac{CIF_{i}}{(1 + r)^{i}} – I \tag{3}
\]

割引率の実態は投資に対する期待利回りなので、NPVが0のときは、その投資の利回りが期待利回りと等しいことを意味する。すなわち、「期待通り」ということである。したがって、0の場合も含めてNPV≧0ならば投資をすべきということになる。

Excelには、その名もNPV関数というものがあるので、それを使えば、上記のような複雑な式など全く知らなくてもNPVを計算できる。