損益分岐点が \(x_{BEP}\) ，実際値（実際売上高等）が \(x_{A}\) のとき、以下の式で計算されるものを安全余裕率という。

\[
\mathrm{安全余裕率} = \dfrac{x_{A} – x_{BEP}}{x_{A}}
\]

下図から分かるように、分子の \((x_{A} – x_{BEP})\) は、実際値と損益分岐点との距離である。それを実際値に対する率にしたものが安全余裕率だ。安全余裕率が高いということは、実際値が損益分岐点から離れていることを意味する。

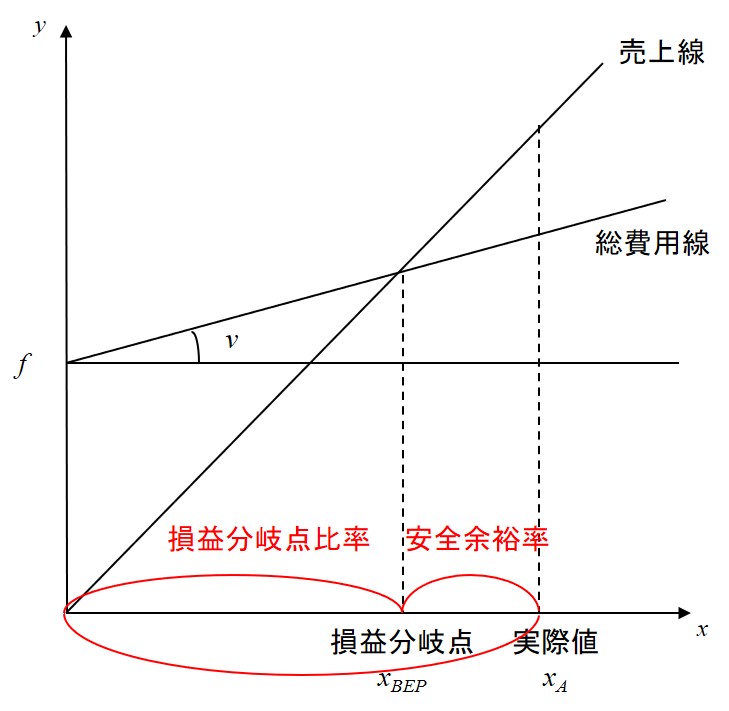
利益が出る出ないだけで言えば、実際値が損益分岐点を超えさえすれば利益は出る。しかし、実際値が損益分岐点に近いと、実際値が少々変動しただけで簡単に損益分岐点を下回って利益がマイナスになってしまう。実際値が損益分岐点から離れていれば、実際値が少々変動したところで損益分岐点は下回らず、利益をプラスに維持できる。

実際値が損益分岐点から離れている状態とは、安全余裕率が高い状態だ。つまり、安全余裕率が高いほど、実際値は損益分岐点から離れているので、変動に対する利益の安定性が高いのである。

一方、以下の式で計算されるものを損益分岐点比率という。

\[
\mathrm{損益分岐点比率} = \dfrac{x_{BEP}}{x_{A}}
\]

これは、文字通り、実際値に対する損益分岐点の比率だ。上図からも分かるように、安全余裕率と損益分岐点比率は合計が常に1になる補数の関係にある。すなわち、安全余裕率が0.2ならば、損益分岐点比率は0.8ということである。