ROIとはReturn On Investmentの頭文字をとったものであり、日本語では投下資本利益率という。

定義式は以下の通りである。

\[
\mathrm{ROI} = \dfrac{\left( \displaystyle \sum_{i=1}^n CIF_{i} – \mathrm{投資額} \right) / \mathrm{評価年数}}{\mathrm{投資額}} \tag{1}
\]

式(1)の \(CIF_{i}\) は投資からもたらされる毎年のキャッシュ・インフローである。分子の \(\sum CIF_{i} – 投資額\) はリターンが投資額を上回るプラスアルファ分の総額だ。それを評価年数（一般的には投資の予想貢献年数）で割ることによって1年あたりの平均プラスアルファ、すなわち平均利益にしている。それを投資額で割ることによって利益率にしている。

ROIには以下のような定義式もある。

\[
\mathrm{ROI} = \dfrac{\left( \displaystyle \sum_{i=1}^n CIF_{i} – \mathrm{投資額} \right) / \mathrm{評価年数}}{\mathrm{投資額} / 2} \tag{2}
\]

式(1)との違いは、式(2)の分母が2で割られているところである。式(1)と区別する場合には、式(1)を総投資利益率、式(2)を平均投資利益率という。

式(1)の総投資利益率は、「初期投資額に対する年平均リターンの率」を計算している。

一方、式(2)の「平均投資利益率」は、「（投資した結果の）資産に対する年平均利益率」を計算している。それは以下のような理由による。

式(2)の分子は以下のように書ける。

\[
\mathrm{式(2)の分子} = \dfrac{\displaystyle \sum_{i=1}^{n} CIF_{i}}{\mathrm{評価年数}} – \dfrac{\mathrm{投資額}}{\mathrm{評価年数}} \tag{3}
\]

残存価額0の定額法を前提とすると、式(3)の第2項は1年あたりの減価償却費を意味するので、式(3)は年平均利益を計算していることに相当する。

一方、減価償却が進むと貸借対照表における資産の計上額は、取得価額（＝投資額）から0まで一定額ずつ減少していくので、貸借対照表に計上される資産の平均額は \(\mathrm{投資額} / 2 \) になる。

したがって、式(3)は資産に対する年平均利益率という意味になるのである。平均投資利益率は、投資が財務諸表に与えるインパクトを分析したい場合などに適している。

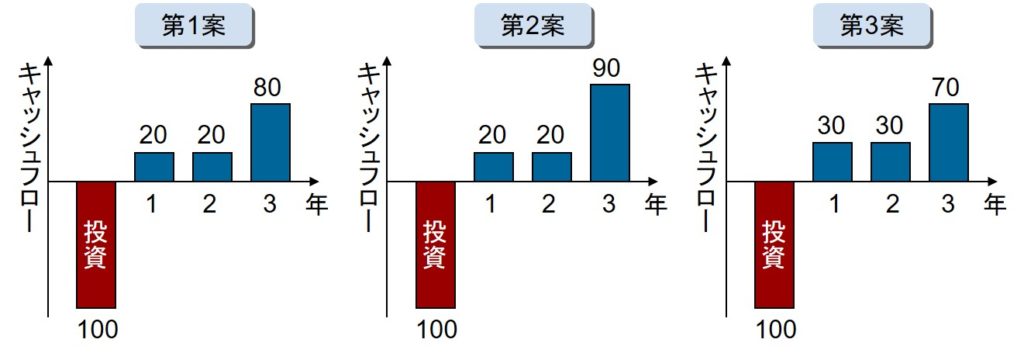
ROIは、回収期間法では評価できなかった収益性を評価できるという長所があるが、リターンのタイミングの違いは評価できない。たとえば、下図を総平均利益率で評価した場合、リターンのプラスアルファが異なる第1案と第2案のROIはそれぞれ6.7%, 10.0%と評価できる。しかし、リターンの総額が同じでも、そのタイミングが異なる第2案と第3案は、いずれもROIが10.0%となり、評価できない。