最小自乗法は、プロットされた複数の点を近似する直線を、数学的に求める方法である。

最小自乗法の基本的考え方は、プロットされたそれぞれの点と直線との距離の合計が最小となるような直線を求めようというものだ。距離の合計が最小ということは、プロットされた各点の最も近くを通っていると考えられる。

具体的には以下のように近似直線を求める。下図のように、\(n\) 個の実績データ \((x_{i}, y_{i}) (i = 1, 2, \cdots, n)\) に対して、これらの点を近似する直線を

\[
y = a + bx
\]

とする。

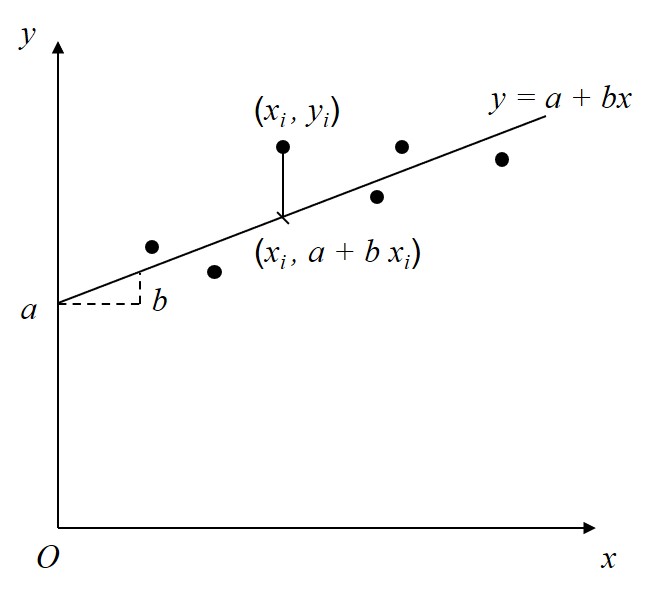
このとき、点 \((x_{i}, y_{i})\) から \(y\) 軸に平行に引いた直線が近似直線と交わる点は \((x_{i}, a + bx_{i})\) なので、2つの点の距離の2乗の和 \(u\) は以下のようになる。

\[
u = \displaystyle \sum_{i=1}^n (a + bx_{i} – y_{i})^2
\]

座標の差を2乗するのは、正にも負にもなり得る座標の差をすべて正にするための数学的な工夫である。「最小自乗法」という名前の由来はここから来ている。

この \(u\) を最小にする \(a\) と \(b\) を求める。そのためには、\(u\) を \(a\) と \(b\) でそれぞれ微分（正確には偏微分）したものが0となる \(a, b\) を求めればよい。

\begin{eqnarray}
\begin{array}{c}
\left\{
\begin{array}{l}
\dfrac{\partial u}{\partial a}
= \displaystyle \sum_{i=1}^n 2\left(a + bx_{i} – y_{i}\right)
= 2\left( na + b \displaystyle \sum_{i=1}^n x_{i} – \displaystyle \sum_{i=1}^n y_{i} \right) = 0 \\
\dfrac{\partial u}{\partial b}
= \displaystyle \sum_{i=1}^n 2\left(a + bx_{i} – y_{i}\right) x_{i}
= 2\left( a\displaystyle \sum_{i=1}^n x_{i} + b \displaystyle \sum_{i=1}^n x_{i}^{2} – \displaystyle \sum_{i=1}^n x_{i}y_{i} \right) = 0
\end{array}
\right. \\

\therefore
\begin{cases}
na + b \displaystyle \sum_{i=1}^n x_{i} – \displaystyle \sum_{i=1}^n y_{i} = 0 \\
a\displaystyle \sum_{i=1}^n x_{i} + b \displaystyle \sum_{i=1}^n x_{i}^{2} – \displaystyle \sum_{i=1}^n x_{i}y_{i} = 0
\end{cases}
\end{array}
\end{eqnarray}

上記の連立方程式を解くことにより、\(a\)（固定費）と \(b\)（変動費）が求まる。 Excelには、近似直線の \(y\) 切片（ \(a\) に相当）を求めるINTERCEPT関数と、傾き（ \(b\) に相当）を求めるSLOPE関数が用意されている。

実務的には、こららの関数を使って計算できれば、理論的な理解がなくても事足りるだろう。