以下のような赤字企業があるとする。

この企業が赤字から脱却するためには、売上高がいくらになればいいだろうか。

売上高が増えると、それに伴って増加する費用もあるので、話はそれほど簡単ではない。費用のうち、80百万円は変動費である。変動費とは売上高に正比例する費用なので、売上高が400百万円のときに変動費が80百万円ということは、変動費率が80百万円÷400万円＝0.2（一定）ということだ。

固定費は、費用総額480百万円から変動費80百万円を除いた残り400百万円なので、売上高\(x\)（百万円）に対して、総費用\(y\)（百万円）は

\[
y = 0.2x + 400
\]

と表現できる。これを売上高 \(x\) が追い抜けば利益が出る。

これを図示すれば下図のようになる。

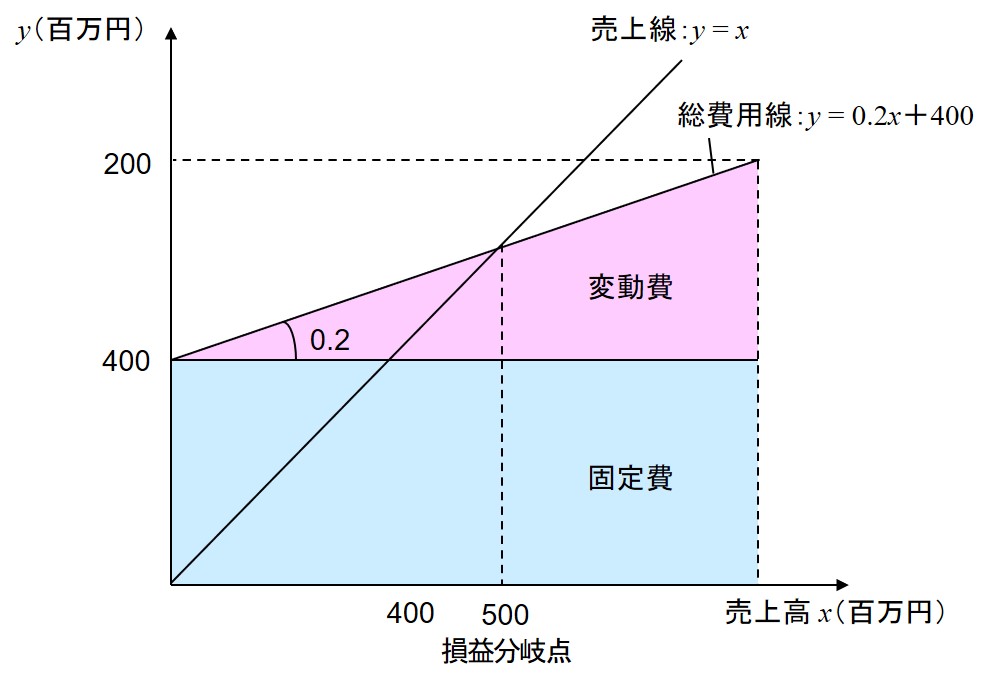
売上線 \(y = x\) が総費用線を追い抜く点を損益分岐点（Break Even Point）という。「損と益の分かれ目」ということだ。

一般に、変動費率を \(v\) 、固定費を \(f\) とすれば、損益分岐点は売上高と総費用が同額になる点なので、以下のように求められる。

\begin{align}
x = vx + f \\
\therefore x = \dfrac{f}{1 – v}
\end{align}

分母の \((1 – v)\) は、限界利益率または貢献利益率という。